Liczby zespolone Liczby zespolone: Są to liczby zespolone, więc jest jest to sprzeczne. Rozwiązać równanie: x²−2x+2=0 Delta wychodzi −4, jak dalej to rozwiązać?

ZKS: i² = −1 więc skorzystaj z tego.

Artur z miasta Neptuna: x²−2x+2 = 0 (x−(1−i))(x−(1+i)) = 0

Liczby zespolone: więc moduł z delty będzie równy ±2i?

Liczby zespolone: Mam takie zadanie: z²−(2−+i)−1+7i=0 Obliczając deltę wychodzi: 7−24i w zadaniu dalej jest obliczone, że to jest równe (4−3i)² czy trzeba to tak dalej obliczać?

Liczby zespolone: halo?

Sławek: Czy to równanie jest dobrze napisane?

Liczby zespolone: Tak, to równanie jest na 100% dobrze napisane

ICSP: taa. Ja widzę przynajmniej dwa błędy

Bart: Przykład przepisane jest z książki. Algebra liniowa Jerzy Topp dział Liczby zespolone strona 32, przykład 35 Rozwiązać równanie x²−2x+x=0

ICSP: jakie tu liczby zespolone? x² − 2x + x = 0 x² − x = 0 x(x−1) = 0 x = 0 v x = 1

Bart: poprawka, zamiast x²−2x+X=0 powinno być x²−2x+2=0 (na końcu +2) delta wychodzi −4. mała delta zatem ±2j

Liczby zespolone: Więc jak to będzie?

ICSP: x² − 2x + 2 = 0 Δ = 4 − 8 = − 4 √Δ = {−2i ; 2i} x₁ = 1 + i x₂ = 1 − i

Sławek: Pytanie dotyczyło postu z 5 lut 13:36.

Liczby zespolone: Mając równanie z⁴−30z²+289=0 w=z² w²−30w+289=0 Δ=−256 √Δ=±16 w₁=15−8i w₂=15+8i w odpowiedzi mam z₁ =4−i, z₂=−4+i, z₃=4+i, z₄=−4−i jak rozłożyć w₁ i w₂ na te 4 pierwiastki?

Liczby zespolone: Faktycznie, przykład jest źle przepisany. Poprawny to: z²−(2+i)z−1+7i=0 Wszystko wiem jak zrobić, wiem że trzeba skorzystać ze wzoru skróconego mnożenia, ale w jaki sposób przejść z postaci 7−24i do (4−3i)² to nie mam pojęcia, mógłby ktoś w zrozumiały sposób wytłumaczyć to?

ICSP: 7 − 24i = 16 − 4 * 3i * 2 − 9 = 4² − 4 * 2 * 3i + (3i)² = (4 − 3i)²

Wojtek: Cześć podepnę się do tego tematu z moim zadaniem, nie wiem jak je rozwiązać Na płaszczyźnie zespolonej narysować zbiory:

	1−z
{z∊C: Re		=1}
	1+z

ICSP: podstawiłeś już x+yi za z ?

Sławek: https://matematykaszkolna.pl/forum/125442.html

Wojtek: tak podstawilem i wychodzi tak jak w linku ale nie wiem jak narysowac wogóle co z tym dalej zrobić

Sławek:

	1−x−iy
Re		= 1
	1+x+iy

Sławek: Tam jest błąd powinno być jak wyżej.

Liczby zespolone: Mając równanie z⁴−30z²+289=0 w=z2 w²−30w+289=0 Δ=−256 √Δ=±16 w1=15−8i, w2=15+8i w odpowiedzi mam z1 =4−i, z2=−4+i, z3=4+i, z4=−4−i jak rozłożyć w1 i w2 na te 4 pierwiastki?

Liczby zespolone:

ICSP: zawijaj i szukaj pierwiastków.

Sławek:

	1−x−iy		(1−x−iy)(1+x−iy)
Re		= 1 ⇔ Re		= 1 ⇔
	1+x+iy		(1+x+iy)(1+x−iy)

	−x2−y2+1−2iy		−x2−y2+1
⇔ Re		= 1 ⇔		= 1 ⇔
	(x+1)2+y2		(x+1)2+y2

−x²−y²+1=(x+1)²+y² −x²−y²+1 = x²+2 x+y²+1 x²+y²+x=0

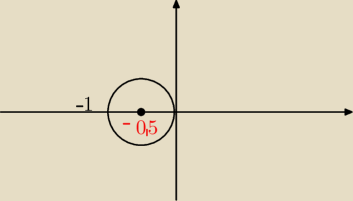
Sławek: x² + x +0,25 −0,25 +y² = 0 (x+0,5)² + y² = (0,5)² okrąg o promieniu 0.5 i środku w punkcie (−0.5, 0)

Sławek: 5

Wojtek: a w tym przykładzie i czy w ogóle mogę mnożyć przez sprzeżenie mianownika

Wojtek: http://www.wolframalpha.com/input/?i=Re+%5B%281-z%29%2F%281%2Bz%29%5D%3D1 w wolfram alfa wychodzi inaczej czyli cos nie tak

Sławek: A dlaczego nie?

Wojtek: bo zmieni sie wartosc wyrazenia i dlatego ja nie monozylem przez sprzezenie i wyszlo mi jak z=0 i taki sam wynik wychozi w wolframaalpha

Sławek: A słyszałeś coś na temat rozszerzania ułamków?

Wojtek: no tak slyszalem

Sławek:

	a+ib		c−id
to jak przemnożysz		przez		to zmieni się wartość wyrażenia?
	c+id		c−id

Sławek: A tak wracając do Wolframalpha, rozbij zadanie części i wyjdzie to samo co u mnie. http://www.wolframalpha.com/input/?i=%281-x-iy%29%2F%281%2Bx%2Biy%29%3D1 http://www.wolframalpha.com/input/?i=-x^2%2F%28%28x%2B1%29^2%2By^2%29-y^2%2F%28%28x%2B1%29^2%2By^2%29%2B1%2F%28%28x%2B1%29^2%2By^2%29+%3D+1

Wojtek: no nie

Wojtek: ale z =0

Sławek: Sorry, ja wymiękam.